如图, 为双曲线 : 的右焦点。 为双曲线 右支上一点,且位于 轴上方, 为左准线上一点, 为坐标原点。已知四边形 为平行四边形, .
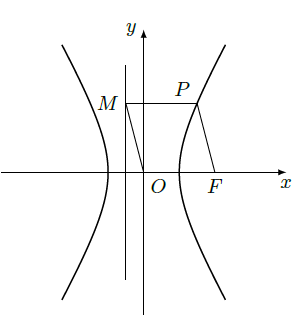
(Ⅰ)写出双曲线
的离心率
与
的关系式;
(Ⅱ)当
时,经过焦点
且品行于
的直线交双曲线于
、
点,若
,求此时的双曲线方程.
推荐套卷
如图, 为双曲线 : 的右焦点。 为双曲线 右支上一点,且位于 轴上方, 为左准线上一点, 为坐标原点。已知四边形 为平行四边形, .

(Ⅰ)写出双曲线
的离心率
与
的关系式;
(Ⅱ)当
时,经过焦点
且品行于
的直线交双曲线于
、
点,若
,求此时的双曲线方程.