本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
从数列 中取出部分项,并将它们按原来的顺序组成一个数列,称之为数列
中取出部分项,并将它们按原来的顺序组成一个数列,称之为数列 的一个子数列.
的一个子数列.
设数列 是一个首项为
是一个首项为 、公差为
、公差为

 的无穷等差数列.
的无穷等差数列.
(1)若 ,
, ,
, 成等比数列,求其公比
成等比数列,求其公比 .
.
(2)若 ,从数列
,从数列 中取出第2项、第6项作为一个等比数列的第1项、第2项,试问该数列是否为
中取出第2项、第6项作为一个等比数列的第1项、第2项,试问该数列是否为 的无穷等比子数列,请说明理由.
的无穷等比子数列,请说明理由.
(3)若 ,从数列
,从数列 中取出第1项、第
中取出第1项、第
 项(设
项(设 )作为一个等比数列的第1项、第2项.求证:当
)作为一个等比数列的第1项、第2项.求证:当 为大于1的正整数时,该数列为
为大于1的正整数时,该数列为 的无穷等比子数列.
的无穷等比子数列.
相关知识点
推荐套卷
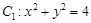 与
与 轴的左右交点分别为
轴的左右交点分别为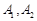 ,直线
,直线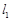 经过
经过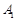 ,直线
,直线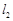 经过
经过 ,
,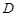 为
为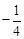 .
. 在圆
在圆 上,
上, ,且
,且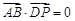 ,当
,当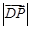 最大时,求弦
最大时,求弦 的长度.
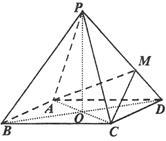
的长度.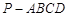 ,底面
,底面 是边长为2的菱形,
是边长为2的菱形,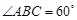 ,
,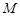 为侧棱
为侧棱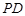 的三等分点(靠近
的三等分点(靠近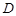 点),
点),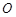 为
为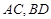 的交点,且
的交点,且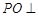 面
面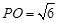 .
.
 ,且
,且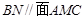 ,确定点
,确定点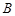 到平面
到平面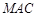 的距离.
的距离.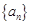 的前
的前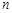 项和为
项和为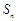 ,
,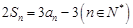 .
.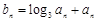 ,求数列
,求数列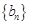 的的前
的的前 .
.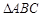 中,角
中,角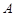 .
.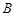 .
.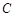 所对的边分别为
所对的边分别为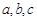 ,且满足
,且满足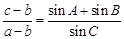 .
.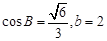 ,求
,求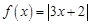 .
.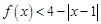 ;
;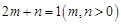 ,若
,若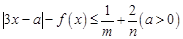 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号