如图中心在原点，焦点在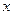
轴上的椭圆，离心率
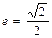，且经过抛物线
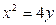的焦点.
（I）求椭圆的标准方程；
（II）若过点B（2，0）的直线L（斜率不等于零）与椭圆交于不同的两点E、F（E在B、F之间），试求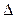
OBE与OBF面积1：2，求直线L的方程。
 |
．
取到极大值,
取到极小值,且
恒成立.
的取值范围;
,求证:
中, 
.
;
上确定一点P,使直线
与平面
所成角的正弦等于
.
中,
(2)求:
.
是
的充要条件;
时, 
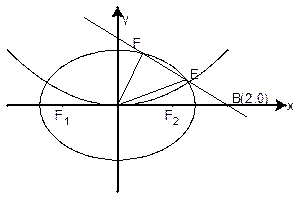的取值范围.推荐套卷
如图中心在原点，焦点在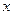轴上的椭圆，离心率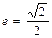，且经过抛物线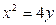的焦点.
（I）求椭圆的标准方程；
（II）若过点B（2，0）的直线L（斜率不等于零）与椭圆交于不同的两点E、F（E在B、F之间），试求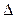OBE与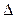OBF面积1：2，求直线L的方程。
|
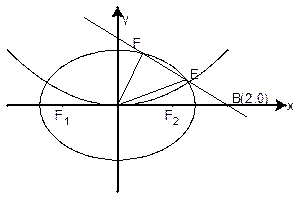粤公网安备 44130202000953号