如图，矩形BCC1B1所在平面垂直于三角形AB
C所在平面，BB1=CC
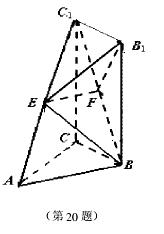
1=AC=2，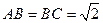
，又E、F分别是C1A和C1B的中点。
（1）求证：EF//平面ABC；
（2）求证：平面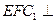
平面C1CBB1；
（3）求异面直线AB与EB1所成的角。
，
的图象.
，求函数y＝
＋
，x∈
的最大值与最小值．
的图象；（2）利用图象回答：
取何值时
值与之对应？
是奇函数，
在
的单调性，并利用定义加以证明
是定义在
上增函数，且
，求x的取值范围.推荐套卷
如图，矩形BCC1B1所在平面垂直于三角形ABC所在平面，BB1=CC1=AC=2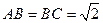，，又E、F分别是C1A和C1B的中点。
（1）求证：EF//平面ABC；
（2）求证：平面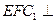平面C1CBB1；
（3）求异面直线AB与EB1所成的角。
粤公网安备 44130202000953号