北京2008年第29届奥运会开幕式上举行升旗仪式，在坡度15°的看台上，在同一列上的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°，第一排和最后一排的距离为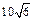
米（如图所示），旗杆底部与第一排在一个水平面上。若国歌长度约为50秒，问：升旗手应以多大的速度（米/秒）匀速升旗？
相关试题
，x∈R，试讨论f（x）的奇偶性，并求f（x）的最小值．
，求当x
0时，f（x）的解析式．
,求a的取值范围．
。
，（1）用列举法表示集合A；（2）写出集合A的所有子集相关知识点
推荐套卷
北京2008年第29届奥运会开幕式上举行升旗仪式，在坡度15°的看台上，在同一列上的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°，第一排和最后一排的距离为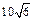米（如图所示），旗杆底部与第一排在一个水平面上。若国歌长度约为50秒，问：升旗手应以多大的速度（米/秒）匀速升旗？
粤公网安备 44130202000953号