对于函数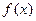
，若存在
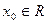，使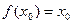
成立，则称点
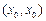为函数的不动点。
（1）已知函数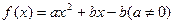
有不动点（1，1）和（-3，-3）求
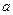与
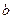的值；
（2）若对于任意实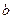数，函数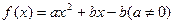总有两个相异的不动点，求 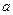的取值范围；
（3）若定义在实数集R上的奇函数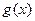
存在（有限的）
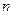个不动点，求证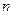：必为奇数。
满足
，
，求
的值
是边长为
的正方形
内或边上一动点，
是
中点，求
最大值
的速度向该容器注水，当水深
时，求水面上升的速度
，
，
，
,求数列
，
通项公式
中，三边为
，且
，
，求△推荐套卷
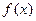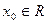对于函数，若存在 ，使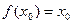成立，则称点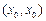为函数的不动点。
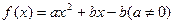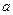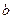（1）已知函数有不动点（1，1）和（-3，-3）求与的值；
（2）若对于任意实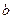数，函数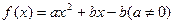总有两个相异的不动点，求 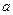的取值范围；
（3）若定义在实数集R上的奇函数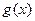存在（有限的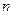） 个不动点，求证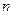：必为奇数。
粤公网安备 44130202000953号