已知数列{an}满足a1＝2，对于任意的n∈N，都有an＞0，且(n＋1)a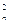
＋anan＋1－na
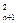＝0，又知数列{bn}:b1＝2n－1＋1
(1)求数列{an}的通项an以及它的前n项和Sn；
(2)求数列{bn}的前n项和Tn；
(3)猜想Sn和Tn的大小关系，并说明理由.
相关试题
的直线的方程.
中，
⊥平面
，
，
为
上的点，且
⊥平面
.
⊥平面
；
的体积．推荐套卷
已知数列{an}满足a1＝2，对于任意的n∈N，都有an＞0，且(n＋1)a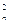＋anan＋1－na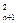＝0，又知数列{bn}:b1＝2n－1＋1
(1)求数列{an}的通项an以及它的前n项和Sn；
(2)求数列{bn}的前n项和Tn；
(3)猜想Sn和Tn的大小关系，并说明理由.
粤公网安备 44130202000953号