（本小题共13分）
已知如图(1)，正三角形ABC的边长为2a,CD是AB边上的高，E、F分别是AC和
BC边上的点，且满足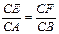
，现将△ABC沿CD翻折成直二面角A-DC-B,如图（2）.
(Ⅰ) 试判断翻折后直线AB与平面DEF的位置关系，并说明理由；
(Ⅱ) 求二面角B-AC-D的平面角的正切值.
 |
|||
 |
|||
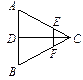图（1） 图（2）
≥m
+n
.
+
≥
+
.推荐套卷
（本小题共13分）
已知如图(1)，正三角形ABC的边长为2a,CD是AB边上的高，E、F分别是AC和
BC边上的点，且满足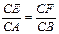，现将△ABC沿CD翻折成直二面角A-DC-B,如图（2）.
(Ⅰ) 试判断翻折后直线AB与平面DEF的位置关系，并说明理由；
(Ⅱ) 求二面角B-AC-D的平面角的正切值.
|
|||
|
|||
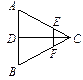图（1） 图（2）
粤公网安备 44130202000953号