如果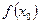 是函数
是函数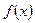 的一个极值,称点
的一个极值,称点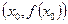 是函数
是函数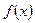 的一个极值点.已知函数
的一个极值点.已知函数
(1)若函数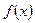 总存在有两个极值点
总存在有两个极值点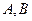 ,求
,求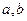 所满足的关系;
所满足的关系;
(2)若函数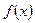 有两个极值点
有两个极值点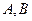 ,且存在
,且存在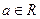 ,求
,求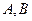 在不等式
在不等式 表示的区域内时实数
表示的区域内时实数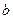 的范围.
的范围.
(3)若函数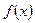 恰有一个极值点
恰有一个极值点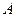 ,且存在
,且存在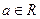 ,使
,使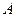 在不等式
在不等式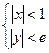 表示的区域内,证明:
表示的区域内,证明: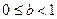 .
.
推荐套卷
如果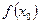 是函数
是函数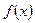 的一个极值,称点
的一个极值,称点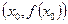 是函数
是函数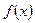 的一个极值点.已知函数
的一个极值点.已知函数
(1)若函数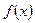 总存在有两个极值点
总存在有两个极值点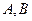 ,求
,求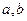 所满足的关系;
所满足的关系;
(2)若函数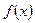 有两个极值点
有两个极值点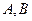 ,且存在
,且存在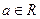 ,求
,求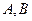 在不等式
在不等式 表示的区域内时实数
表示的区域内时实数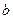 的范围.
的范围.
(3)若函数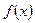 恰有一个极值点
恰有一个极值点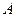 ,且存在
,且存在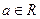 ,使
,使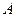 在不等式
在不等式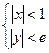 表示的区域内,证明:
表示的区域内,证明: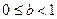 .
.