某射击测试规则为：每人最多射击3次，击中目标即终止射击，第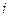
次击中目标得
分，3次均未击中目标得0分．已知某射手每次击中目标的概率为0.8，其各次射击结果互不影响．
（Ⅰ）求该射手恰好射击两次的概率；
（Ⅱ）该射手的得分记为
，求随机变量
的分布列及数学期望．
相关试题
中，角A,B,C所对的边分别为a,b,c, 已知a,b,c成等比数列，且
．
，求
：
，直线
：
交
，交准线于点
．过点
与抛物线
（
轴交于点
．
的取值范围．
，函数
．
时，求函数
的最小值；
时，讨论
的图象与
的图象的公共点个数．
中，△
是边长为
的正三角形，
， 
，
分别为
，
的中点，
，
． 
平面
；
与平面
满足：
，
，（
），
，
，
分别是公差不为零的等差数列
的前三项．
的值；
，
，
，
不可能成等比数列.推荐套卷
某射击测试规则为：每人最多射击3次，击中目标即终止射击，第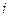次击中目标得
分，3次均未击中目标得0分．已知某射手每次击中目标的概率为0.8，其各次射击结果互不影响．
（Ⅰ）求该射手恰好射击两次的概率；
（Ⅱ）该射手的得分记为
，求随机变量
的分布列及数学期望．
粤公网安备 44130202000953号