、
两个投资项目的利润率分别为随机变量
和
.根据市场分析,
,
的分布列分别为
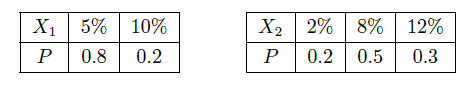
(Ⅰ)在
、
两个项目上各投资
万元,
和
分别表示投资项目
和
所获得的利润,求方差
,
;
(Ⅱ)将
万元投资A项目,
万元投资
项目,
表示投资
项目所得利润的方差与投资
项目所得到利润的方差的和。求
的最小值,并指出
为何值时,
取到最小值。
(注:
)
相关知识点
推荐套卷
 取1个,直到取出红球为止,求甲取球的次数
取1个,直到取出红球为止,求甲取球的次数 的分布列和数学期望.
的分布列和数学期望. ,其中
,其中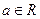
 在
在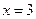 处取得极值,求
处取得极值,求 的值;
的值;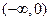 上为增函数,求
上为增函数,求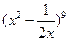 展开式的:
展开式的: 的系数
的系数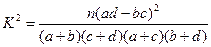

 上是单调函数,求实数
上是单调函数,求实数 的取值范围;
的取值范围; 1时,不等式
1时,不等式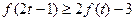 恒成立,求实数
恒成立,求实数 粤公网安备 44130202000953号
粤公网安备 44130202000953号