已知曲线C：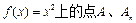
的横坐标分别为1和
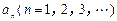，且a1=5，数列{xn}满足xn+1 = tf (xn – 1) + 1（t > 0且
）．设区间
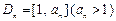，当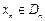
时，曲线C上存在点
使得xn的值与直线AAn的斜率之半相等．
(1)证明：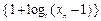
是等比数列；
(2)当
对一切
恒成立时，求t的取值范围；
(3)记数列{an}的前n项和为Sn，当
时，试比较Sn与n + 7的大小，并证明你的结论．
的特征值．
的特征多项式．
，若矩阵M的逆矩阵M－1＝
，求a、b的值．
，N＝
，求MN.
(其中a>0，b>0)．
＋y2＝1，求a、b的值．推荐套卷
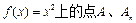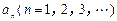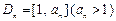已知曲线C：的横坐标分别为1和，且a1=5，数列{xn}满足xn+1 = tf (xn – 1) + 1（t > 0且）．设区间，当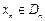时，曲线C上存在点使得xn的值与直线AAn的斜率之半相等．
(1)证明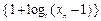：是等比数列；
(2)当对一切恒成立时，求t的取值范围；
(3)记数列{an}的前n项和为Sn，当时，试比较Sn与n + 7的大小，并证明你的结论．
粤公网安备 44130202000953号