(1) 已知动点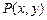
到点
与到直线
的距离相等，求点
的轨迹
的方程；
(2) 若正方形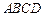
的三个顶点
，
，
(
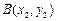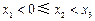)在(1)中的曲线上，设
的斜率为
，
，求
关于的函数解析式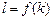
；
(3) 求(2)中正方形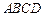面积
的最小值．
，
在函数
的图像上，称
为函数
的一组关于原点的中心对称点，
关于原点的中心对称点有多少组
=
（
的对称中心为
，证明：函数
的图象是一个中心对称图形，并求其对称中心
的定义域为
，若对任意的
，都有
求
范围相关知识点
推荐套卷
(1) 已知动点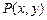到点与到直线的距离相等，求点的轨迹的方程；
(2) 若正方形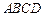的三个顶点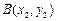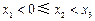，，()在(1)中的曲线上，设的斜率为，，求关于的函数解析式；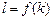
(3) 求(2)中正方形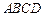面积的最小值．
粤公网安备 44130202000953号