已知
之间满足
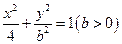
（1）方程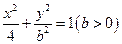表示的曲线经过一点
，求b的值
（2）动点(x,y)在曲线
(b>0)上变化，求x2+2y的最大值；
（3）由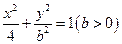能否确定一个函数关系式
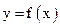，如能，求解析式；如不能，再加什么条件就可使之间建立函数关系，并求出解析式。
相关试题
为奇函数，
,
,求
.
在点（1，f(1))处的切线为
,若
的弦长为2，求a；
与离心率e=
的椭圆C：
交于P、Q两点，直线
，求直线
的导函数
，数列{
}的前n项和为
，点
（n，
的图象上．若
=
（
与
的大小；
试证
推荐套卷
已知之间满足
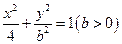
（1）方程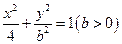表示的曲线经过一点，求b的值
（2）动点(x,y)在曲线(b>0)上变化，求x2+2y的最大值；
（3）由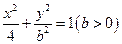能否确定一个函数关系式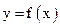，如能，求解析式；如不能，再加什么条件就可使之间建立函数关系，并求出解析式。
粤公网安备 44130202000953号