如图，椭圆的中心在原点，其左焦点
与抛物线
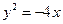的焦点重合，过的直线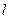
与椭圆交于A、B两点，与抛物线交于C、D两点．当直线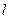与x轴垂直时，
．
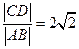（Ⅰ）求椭圆的方程；
（II）求过点O、，并且与椭圆的左准线相切的圆的方程；
（Ⅲ）求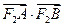
的最大值和最小值．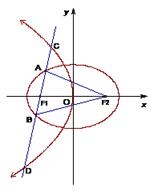
相关试题
中，底面
为矩形，侧面
底面
，
，
．
；
与平面
所成的角为
，求二面角
的大小．
中，角
所对的边分别是
，
.
的值；（2）若
，求
的最小正周期和最小值；并写出
上的单调递增区间
，且A为锐角.
的值域.
； 
.推荐套卷
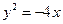如图，椭圆的中心在原点，其左焦点与抛物线的焦点重合，过的直线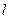与椭圆交于A、B两点，与抛物线交于C、D两点．当直线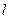与x轴垂直时，．
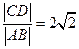（Ⅰ）求椭圆的方程；
（II）求过点O、，并且与椭圆的左准线相切的圆的方程；
（Ⅲ）求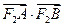的最大值和最小值．
粤公网安备 44130202000953号