如图，已知正四棱柱ABCD—A1B1C1D1中，底面边长AB＝2，侧棱BB1的长为4，过点B作B1C的垂线交侧棱CC1于点E，交B1C于点F，
（1）求证：A1C⊥平面BDE；
（2）求A1B与平面BDE所成角的正弦值。
（3）设F是CC1上的动点(不包括端点C)，求证：△DBF是锐角三角形。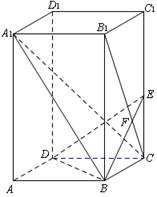
相关试题
，
，其中
，集合
，全集
。
，求
的值；
，求
。
是一次函数，且
.
时，函数
恒成立，求实数
的取值范围
，求函数
的定义域； 
，求
表示）；
，使得
，并且
，若存在，求出实数
，当
时，
有最小值
；
的值； （2）求满足
的
的集合
;
分以下（包括
推荐套卷
如图，已知正四棱柱ABCD—A1B1C1D1中，底面边长AB＝2，侧棱BB1的长为4，过点B作B1C的垂线交侧棱CC1于点E，交B1C于点F，
（1）求证：A1C⊥平面BDE；
（2）求A1B与平面BDE所成角的正弦值。
（3）设F是CC1上的动点(不包括端点C)，求证：△DBF是锐角三角形。
粤公网安备 44130202000953号