如图，在某城市中，Ｍ，Ｎ两地之间有整齐的方格形道路网，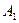
、
、
、
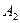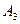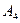是道路网中位于一条对角线上的４个交汇处，今在道路网Ｍ、Ｎ处的甲、乙两人分别要到Ｍ，Ｎ处，他们分别随机地选择一条沿街的最短路径，同时以每１０分钟一格的速度分别向Ｎ，Ｍ处行走，直到到达Ｎ，Ｍ为止。
（１）求甲经过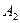的概率；
（２）求甲、乙两人相遇经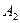点的概率；
（３）求甲、乙两人相遇的概率；
相关试题
为等差数列，
是等差数列的前
项和，已知
，
.
；
为数列
的前
的三个内角
所对的边分别为
,且满足
.
的大小；
，
，求
的值.
，
，且
.
的最小正周期及单调增区间；
，求函数
与
的夹角为
，
，
，求
的值.
.
，求曲线
在点
处的切线方程；
的取值范围；
，且至少存在一点
，使得
成立，求实数推荐套卷
如图，在某城市中，Ｍ，Ｎ两地之间有整齐的方格形道路网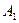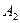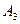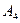，、、、是道路网中位于一条对角线上的４个交汇处，今在道路网Ｍ、Ｎ处的甲、乙两人分别要到Ｍ，Ｎ处，他们分别随机地选择一条沿街的最短路径，同时以每１０分钟一格的速度分别向Ｎ，Ｍ处行走，直到到达Ｎ，Ｍ为止。
（１）求甲经过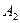的概率；
（２）求甲、乙两人相遇经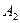点的概率；
（３）求甲、乙两人相遇的概率；
粤公网安备 44130202000953号