（本小题满分13分）
甲、乙两人进行五局三胜制的游戏（即先胜三局者获胜），若甲每局胜率为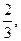
乙每局胜率为
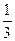，设每局比赛之间相互没有影响。
（1）恰好第五局甲胜的概率；
（2）记ξ为本次游戏的局数，求ξ的概率分布列和数学期望。
相关试题
的展开式中，已知第三项与第五项的系数相等．
展开式中的系数最大的项和系数最小的项；
展开式中含
项的系数
，
为虚数单位，
.
纯虚数，求
的值；
，求
，函数
．
的单调区间和值域；
，若
，总
，使得
成立，求
的取值范围；
，证明：
．
中，满足
,
是
中点.
,求向量
与向量
的夹角的余弦值；
是线段
上任意一点，且
，求
的最小值；
是
,
，
,求
的最小值.
对任意的
，都有
成立，且当
时，
．
的值；（2）求证：
是R上的增函数；
，不等式
对任意的
恒成立，求实数
的取值范围．推荐套卷
（本小题满分13分）
甲、乙两人进行五局三胜制的游戏（即先胜三局者获胜），若甲每局胜率为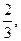乙每局胜率为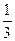，设每局比赛之间相互没有影响。
（1）恰好第五局甲胜的概率；
（2）记ξ为本次游戏的局数，求ξ的概率分布列和数学期望。
粤公网安备 44130202000953号