围建一个面积为
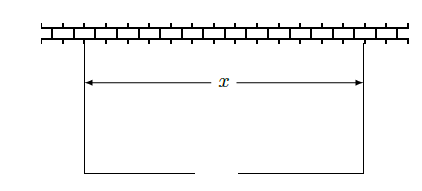
的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为
的进出口,如图所示,已知旧墙的维修费用为45元
,新墙的造价为180元
,设利用的旧墙的长度为
(单位:元).
(Ⅰ)将
表示为
的函数;
(Ⅱ)试确定
,使修建此矩形场地围墙的总费用最小,并求出最小总费用.
推荐套卷
围建一个面积为
的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为
的进出口,如图所示,已知旧墙的维修费用为45元
,新墙的造价为180元
,设利用的旧墙的长度为
(单位:元).

(Ⅰ)将
表示为
的函数;
(Ⅱ)试确定
,使修建此矩形场地围墙的总费用最小,并求出最小总费用.