已知以原点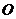 为中心的椭圆的一条准线方程为
为中心的椭圆的一条准线方程为 ,离心率
,离心率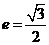 ,
,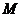 是椭圆上的动点。
是椭圆上的动点。
(Ⅰ)若 的坐标分别是
的坐标分别是 ,求
,求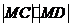 的最大值;
的最大值;
(Ⅱ)如题(20)图,点 的坐标为
的坐标为 ,
,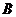 是圆
是圆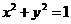 上的点,
上的点,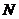 是点
是点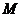 在
在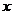 轴上的射影,点
轴上的射影,点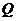 满足条件:
满足条件: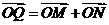 ,
,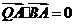 ,求线段
,求线段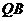 的中点
的中点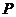 的轨迹方程。
的轨迹方程。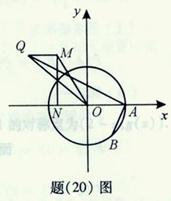
推荐套卷
已知以原点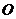 为中心的椭圆的一条准线方程为
为中心的椭圆的一条准线方程为 ,离心率
,离心率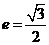 ,
,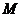 是椭圆上的动点。
是椭圆上的动点。
(Ⅰ)若 的坐标分别是
的坐标分别是 ,求
,求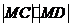 的最大值;
的最大值;
(Ⅱ)如题(20)图,点 的坐标为
的坐标为 ,
,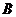 是圆
是圆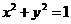 上的点,
上的点,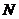 是点
是点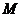 在
在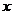 轴上的射影,点
轴上的射影,点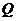 满足条件:
满足条件: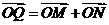 ,
,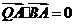 ,求线段
,求线段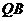 的中点
的中点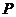 的轨迹方程。
的轨迹方程。