如图：已知直三棱柱ABC—A1B1C1，AB＝AC，F为棱BB1上一点，BF∶FB1＝2∶1，BF＝BC＝2a。
（I）若D为BC的中点，E为AD上不同于A、D的任意一点，证明EF⊥FC1；
（II）试问：若AB＝2a，在线段AD上的E点能否使EF与平面BB1C1C成60°角，为什么？证明你的结论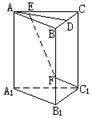
相关试题
求
的值．
S，B
B)∩A＝{1,2,3}，
A，
，求a的取值范围.推荐套卷
如图：已知直三棱柱ABC—A1B1C1，AB＝AC，F为棱BB1上一点，BF∶FB1＝2∶1，BF＝BC＝2a。
（I）若D为BC的中点，E为AD上不同于A、D的任意一点，证明EF⊥FC1；
（II）试问：若AB＝2a，在线段AD上的E点能否使EF与平面BB1C1C成60°角，为什么？证明你的结论
粤公网安备 44130202000953号