在边长为a的正三角形的三个角处各剪去一个四边形．这个四边形是由两个全等的直角三角形组成的，并且这三个四边形也全等，如图①．若用剩下的部分折成一个无盖的正三棱柱形容器，如图②．则当容器的高为多少时，可使这个容器的容积最大，并求出容积的最大值．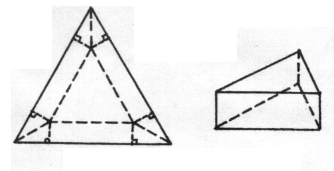
图① 图②
，
，
的夹角为θ，且tanθ=
的值；（2）求
的值.
的前n项和记为
，点（n，
（
）上
，求数列
的前n项和
的值.
中，内角
的对边分别为
，满足
．
的度数； 
求
中，内角
所对的边长分别为
，
，
，
．
和
的值．推荐套卷
在边长为a的正三角形的三个角处各剪去一个四边形．这个四边形是由两个全等的直角三角形组成的，并且这三个四边形也全等，如图①．若用剩下的部分折成一个无盖的正三棱柱形容器，如图②．则当容器的高为多少时，可使这个容器的容积最大，并求出容积的最大值．
图① 图②
粤公网安备 44130202000953号