（本小题共12分） 在平面直角坐标系中,已知An(n,an)、Bn(n,bn)、Cn(n-1,0)(n∈N*)，满足向量
与向量
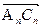共线，且点An(n,an) (n∈N*)都在斜率为2的同一条直线l上. 若
a1=-3，b1=10
（1）求数列{an}与{ bn }的通项公式；
（2）求当n取何值时△AnBnCn的面积Sn最小，并求出Sn的这个最小值。
相关试题
时，若“p且q”为真命题，求实数
的取值范围；
的取值范围.
的焦点分别是
和
，已知椭圆的离心率
过中心
作直线与椭圆交于A，B两点，
的面积是20，
的值（2）直线AB的方程
上，M
垂直于椭圆焦点所在的直线，垂足为
为线段M
的中点，求
表示的平面区域，并求平面区域面积。
的前n项和为
，已知
，
。求
和推荐套卷
（本小题共12分） 在平面直角坐标系中,已知An(n,an)、Bn(n,bn)、Cn(n-1,0)(n∈N*)，满足向量与向量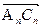共线，且点An(n,an) (n∈N*)都在斜率为2的同一条直线l上. 若a1=-3，b1=10 （1）求数列{an}与{ bn }的通项公式；
（2）求当n取何值时△AnBnCn的面积Sn最小，并求出Sn的这个最小值。
粤公网安备 44130202000953号