如图，PC⊥平面ABC，∠ACB=90°，D为AB中点，
AC=BC=PC=2．
(Ⅰ)求证：AB⊥平面PCD；
(Ⅱ)求异面直线PD与BC所成角的大小；
(Ⅲ)设M为线段PA上的点，且AP=4AM，求点A到平面BCM的距离．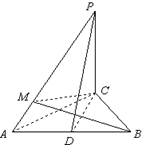
相关试题
满足：
，
.
.
及
；
,
（
），求数列
的前
项和
.
中,BC=a,AC=b,a,b是方程
的两个根，且2COS(A+B)=1.
是首项是2，公比为q的等比数列，其中
是
与
的等差中项. 
.
项的和 
，求数列的通项公式.推荐套卷
如图，PC⊥平面ABC，∠ACB=90°，D为AB中点，
AC=BC=PC=2．
(Ⅰ)求证：AB⊥平面PCD；
(Ⅱ)求异面直线PD与BC所成角的大小；
(Ⅲ)设M为线段PA上的点，且AP=4AM，求点A到平面BCM的距离．
粤公网安备 44130202000953号