已知函数f（x）=x2－4，设曲线y＝f（x）在点（xn，f（xn））处的切线与x轴的交点为（xn+1,0）（n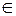
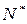），其中
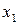为正实数.
（Ⅰ）用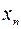
表示xn+1；
（Ⅱ）若a1=4，记an=lg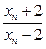
，证明数列｛
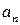｝成等比数列，并求数列｛xn｝的通项公式；
（Ⅲ）若x1＝4，bn＝xn－2，Tn是数列｛bn｝的前n项和，证明Tn<3.
.
，b=2，△ABC的面积S=
，求第三边c.
和
是两个非零的已知向量，当
的模取最小值时，（1）求t的值；（2）已知
角，求证
，C=30
，求A、B.
，
，
，
；推荐套卷
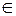
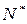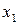已知函数f（x）=x2－4，设曲线y＝f（x）在点（xn，f（xn））处的切线与x轴的交点为（xn+1,0）（n），其中为正实数.
（Ⅰ）用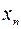表示xn+1；
（Ⅱ）若a1=4，记an=lg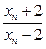，证明数列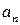｛｝成等比数列，并求数列｛xn｝的通项公式；
（Ⅲ）若x1＝4，bn＝xn－2，Tn是数列｛bn｝的前n项和，证明Tn<3.
粤公网安备 44130202000953号