.在直角坐标平面中，△ABC的两个顶点为 A（0，－1），B（0, 1）平面内两点G、M同时满足①
, ②
= 
= 
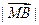③
∥
（1）求顶点C的轨迹E的方程
（2）设P、Q、R、N都在曲线E上 ，定点F的坐标为（
, 0） ，已知
∥
, 
∥
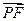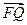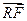且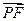·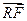= 0.求四边形PRQN面积S的最大值和最小值.
相关试题
是等差数列，
是各项为正
数的等比数列，且
，
，
. 
，求数列
的前
项和
.
是公比大于1的等比数列，
为数列
项和．已知
，且
构成
求数列
的前
．
中，角
所对的边分别是
，
，且满足
；
求角
和边
的大小；
中，
，求通项公式
和前
项和
.
满足
,对于任意
R都有
,且
,令
.
的表达式；
的单调区间；
上的零点个数.推荐套卷
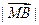.在直角坐标平面中，△ABC的两个顶点为 A（0，－1），B（0, 1）平面内两点G、M同时满足① , ②= = ③∥
（1）求顶点C的轨迹E的方程
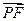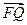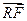（2）设P、Q、R、N都在曲线E上 ，定点F的坐标为（, 0） ，已知∥ , ∥且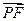·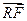= 0.求四边形PRQN面积S的最大值和最小值.
粤公网安备 44130202000953号