学校食堂改建一个开水房,计划用电炉或煤炭烧水,但用煤时也要用电鼓风及时排气,用煤烧开水每吨开水费为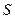 元,用电炉烧开水每吨开水费为
元,用电炉烧开水每吨开水费为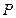 元,
元,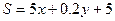 ,
,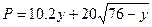 ;其中
;其中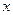 为每吨煤的价格(单位:元),
为每吨煤的价格(单位:元),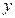 为每百度电的价格(单位:元),如果烧煤时的费用不超过用电炉时的费用,则仍用原备的锅炉烧水,否则就用电炉烧水.
为每百度电的价格(单位:元),如果烧煤时的费用不超过用电炉时的费用,则仍用原备的锅炉烧水,否则就用电炉烧水.
(1)如果两种方法烧水费用相同,试将每吨煤的价格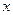 表示为每百度电价
表示为每百度电价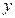 的函数;
的函数;
(2)如果每百度电价不低于60元,则用煤烧水时每吨煤的最高价格是多少?
推荐套卷
学校食堂改建一个开水房,计划用电炉或煤炭烧水,但用煤时也要用电鼓风及时排气,用煤烧开水每吨开水费为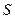 元,用电炉烧开水每吨开水费为
元,用电炉烧开水每吨开水费为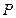 元,
元,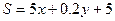 ,
,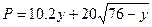 ;其中
;其中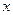 为每吨煤的价格(单位:元),
为每吨煤的价格(单位:元),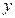 为每百度电的价格(单位:元),如果烧煤时的费用不超过用电炉时的费用,则仍用原备的锅炉烧水,否则就用电炉烧水.
为每百度电的价格(单位:元),如果烧煤时的费用不超过用电炉时的费用,则仍用原备的锅炉烧水,否则就用电炉烧水.
(1)如果两种方法烧水费用相同,试将每吨煤的价格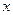 表示为每百度电价
表示为每百度电价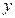 的函数;
的函数;
(2)如果每百度电价不低于60元,则用煤烧水时每吨煤的最高价格是多少?