于定义在D上的函数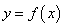 ,若同时满足
,若同时满足
①存在闭区间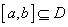 ,使得任取
,使得任取 ,都有
,都有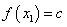 (
( 是常数);
是常数);
②对于D内任意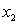 ,当
,当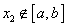 时总有
时总有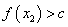 ;
;
则称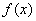 为“平底型”函数.
为“平底型”函数.
(1)判断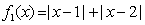 ,
,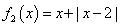 是否是“平底型”函数?简要说明理由;
是否是“平底型”函数?简要说明理由;
(2)设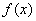 是(1)中的“平底型”函数,若
是(1)中的“平底型”函数,若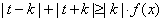 ,(
,(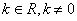 )
)
对一切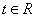 恒成立,求实数
恒成立,求实数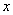 的范围;
的范围;
(3)若 是“平底型”函数,求
是“平底型”函数,求 和
和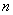 的值.
的值.
推荐套卷
于定义在D上的函数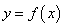 ,若同时满足
,若同时满足
①存在闭区间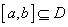 ,使得任取
,使得任取 ,都有
,都有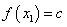 (
( 是常数);
是常数);
②对于D内任意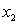 ,当
,当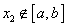 时总有
时总有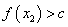 ;
;
则称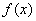 为“平底型”函数.
为“平底型”函数.
(1)判断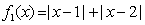 ,
,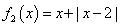 是否是“平底型”函数?简要说明理由;
是否是“平底型”函数?简要说明理由;
(2)设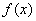 是(1)中的“平底型”函数,若
是(1)中的“平底型”函数,若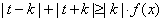 ,(
,(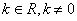 )
)
对一切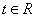 恒成立,求实数
恒成立,求实数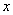 的范围;
的范围;
(3)若 是“平底型”函数,求
是“平底型”函数,求 和
和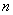 的值.
的值.