一个四棱锥的三视图和直观图如图所示，E为侧棱PD的中点.
（1）求证：PB//平面AEC； 
（2）若F为侧棱PA上的一点，且
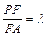， 则为何值时，PA平面BDF？ 并求此时几何体F—BDC的体积．
相关试题
．
，集合
,求
，
.
，当
时，对应
值的集合为
.
的值；（2）若
，求该函数的最值.
；
.
，
，
，
.
； （2）若
，求实数
的取值范围.
的圆
与
轴及直线
均相切，切点分别为
、
，另一圆
与圆
、
．
的平行线
，求直线相关知识点
推荐套卷
一个四棱锥的三视图和直观图如图所示，E为侧棱PD的中点.
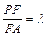（1）求证：PB//平面AEC； （2）若F为侧棱PA上的一点，且， 则为何值时，PA平面BDF？ 并求此时几何体F—BDC的体积．
粤公网安备 44130202000953号