
一个空间几何体 的三视图如图所 示,其中
的三视图如图所 示,其中 分别是
分别是 五点在直立、侧立、水平三个投影面内的投影,且在主视图中,四边形
五点在直立、侧立、水平三个投影面内的投影,且在主视图中,四边形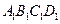 为正方形且
为正方形且 ;在左视图中
;在左视图中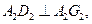 俯视图中
俯视图中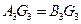 ,
,
(Ⅰ)根据三视图作出空间几何体 的直观图,并标明
的直观图,并标明 五点的位置;
五点的位置;
(Ⅱ)在空间几何体 中,过点
中,过点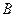 作平面
作平面 的垂线,若垂足H在直线
的垂线,若垂足H在直线 上,求证:平面
上,求证:平面 ⊥平面
⊥平面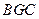 ;
;
(Ⅲ)在(Ⅱ)的条件下,求三棱锥 的体积及其外接球的表面积.
的体积及其外接球的表面积.
推荐套卷

一个空间几何体 的三视图如图所 示,其中
的三视图如图所 示,其中 分别是
分别是 五点在直立、侧立、水平三个投影面内的投影,且在主视图中,四边形
五点在直立、侧立、水平三个投影面内的投影,且在主视图中,四边形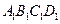 为正方形且
为正方形且 ;在左视图中
;在左视图中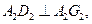 俯视图中
俯视图中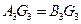 ,
,
(Ⅰ)根据三视图作出空间几何体 的直观图,并标明
的直观图,并标明 五点的位置;
五点的位置;
(Ⅱ)在空间几何体 中,过点
中,过点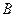 作平面
作平面 的垂线,若垂足H在直线
的垂线,若垂足H在直线 上,求证:平面
上,求证:平面 ⊥平面
⊥平面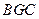 ;
;
(Ⅲ)在(Ⅱ)的条件下,求三棱锥 的体积及其外接球的表面积.
的体积及其外接球的表面积.