某校高二年级有学生1000人,在某次数学考试中,为研究学生的考试情况,需从中抽取40名学生的成绩,
(1)问采用何种抽样方法更合适?
(2)根据所抽取的40名学生成绩,分组在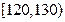 ,
,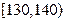 ,
,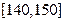 的频率分布直方图中对应的小矩形的高分别是
的频率分布直方图中对应的小矩形的高分别是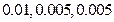 ,问所取的40名学生的成绩不低于
,问所取的40名学生的成绩不低于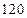 分的共有多少人?
分的共有多少人?
(3)在(2)所求的成绩不低于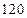 分的学生中任取2人为一组(不分先后),求至少有1人的成绩在
分的学生中任取2人为一组(不分先后),求至少有1人的成绩在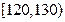 内的概率.
内的概率.
推荐套卷
某校高二年级有学生1000人,在某次数学考试中,为研究学生的考试情况,需从中抽取40名学生的成绩,
(1)问采用何种抽样方法更合适?
(2)根据所抽取的40名学生成绩,分组在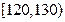 ,
,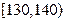 ,
,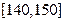 的频率分布直方图中对应的小矩形的高分别是
的频率分布直方图中对应的小矩形的高分别是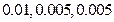 ,问所取的40名学生的成绩不低于
,问所取的40名学生的成绩不低于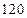 分的共有多少人?
分的共有多少人?
(3)在(2)所求的成绩不低于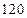 分的学生中任取2人为一组(不分先后),求至少有1人的成绩在
分的学生中任取2人为一组(不分先后),求至少有1人的成绩在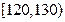 内的概率.
内的概率.