在边长为3的正三角形ABC中，E、F、P分别是AB、AC、BC边上的点，满足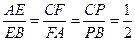
，将
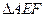沿EF折起到
的位置，使二面角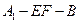
成直二面角，连结
，
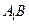（如图）（I）求证：
(Ⅱ)求点B到面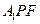
的距离(Ⅲ)求异面直线BP与
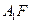所成角的余弦
相关试题
的前
项和
,满足
,
.
的前
；
，证明：
．
（
（
），前
项和为80，其中最大的一项为54，又它的前
项和为6560，求
的内角
所对的边分别为
且
．
的大小；
,求
的最小正周期和图象的对称轴方程；
上的值域．推荐套卷
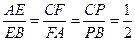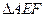在边长为3的正三角形ABC中，E、F、P分别是AB、AC、BC边上的点，满足，将沿EF折起到的位置，使二面角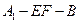成直二面角，连结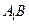，（如图）（I）求证： (Ⅱ)求点B到面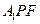的距离(Ⅲ)求异面直线BP与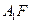所成角的余弦
粤公网安备 44130202000953号