如图,在长方体 中,点
中,点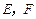 分别在
分别在 上,且
上,且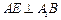 ,
, .
.
(1)求证: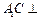 平面
平面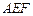 ;
;
(2)若规定两个平面所成的角是这两个平面所组成的二面角中的锐角(或直角),则在空间有定理:若两条直线分别垂直于两个平面,则这两条直线所成的角与这两个平面所成角相等,试根据上述定理,在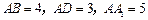 时,求平面
时,求平面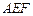 与平面
与平面 所成角的大小.
所成角的大小.
推荐套卷
如图,在长方体 中,点
中,点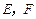 分别在
分别在 上,且
上,且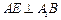 ,
, .
.
(1)求证: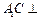 平面
平面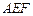 ;
;
(2)若规定两个平面所成的角是这两个平面所组成的二面角中的锐角(或直角),则在空间有定理:若两条直线分别垂直于两个平面,则这两条直线所成的角与这两个平面所成角相等,试根据上述定理,在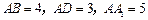 时,求平面
时,求平面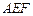 与平面
与平面 所成角的大小.
所成角的大小.