摆地摊的某摊(赌)主拿了8个白的,8个黑的围棋子放在一个口袋里,并规定凡愿意摸彩者每人交一元钱作手续费,然后一次从口袋摸出5个棋子,中彩情况如下:
| 摸棋子 |
5个白 |
4个白 |
3个白 |
其它 |
| 彩金 |
20元 |
2元 |
纪念品(价值5角) |
同乐一次(无任何奖品) |
试计算:
(1)获得20元彩金的概率;
(2)获得2元彩金的概率;
(3)获得纪念品的概率;
(4)按摸彩1000次统计,赌主可望净赚多少钱?
推荐套卷
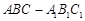 中,侧面
中,侧面 是菱形,
是菱形,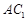 与
与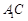 交于点
交于点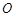 ,E是AB的中点.
,E是AB的中点.
 平面
平面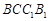 ;
; ,求证:
,求证: .
.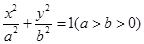 经过点
经过点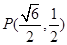 ,离心率为
,离心率为 ,动点M(2,t)(
,动点M(2,t)( ).
).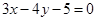 所得的弦长为2的圆的方程;
所得的弦长为2的圆的方程; ,且方程
,且方程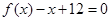 有两个实根
有两个实根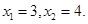
 的解析式;
的解析式;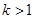 ,解关于
,解关于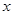 的不等式
的不等式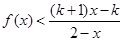 .
. 的顶点是双曲线
的顶点是双曲线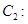
 的中心,而焦点是双曲线的左顶点,
的中心,而焦点是双曲线的左顶点, 时,求抛物线
时,求抛物线 ,求双曲线的渐近线方程和准线的方程.
,求双曲线的渐近线方程和准线的方程. ,下面做投掷这两个正四面体玩具的试验:用(x,y)表示结果,其中x表示第1颗出现的点数(面朝下的数字),y表示第2颗出现的点数(面朝下的数字).
,下面做投掷这两个正四面体玩具的试验:用(x,y)表示结果,其中x表示第1颗出现的点数(面朝下的数字),y表示第2颗出现的点数(面朝下的数字). 或
或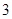 整除”的概率.
整除”的概率. 粤公网安备 44130202000953号
粤公网安备 44130202000953号