设两个非零向量e1和e2不共线.
（1）如果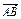
=e1-e2，
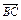=3e1+2e2，
=-8e1-2e2，
求证：A、C、D三点共线；
（2）如果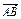=e1+e2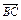，=2e1-3e2，=2e1-ke2，且A、C、D三点共线，求k的值.
使函数
是奇函数。
的函数
的最小值为
，试确定满足
的
的值，并对此时的
的最大值。
的奇偶性。
；（2）
。
的定义域。推荐套卷
设两个非零向量e1和e2不共线.
（1）如果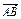=e1-e2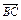，=3e1+2e2，=-8e1-2e2，
求证：A、C、D三点共线；
（2）如果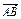=e1+e2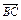，=2e1-3e2，=2e1-ke2，且A、C、D三点共线，求k的值.
粤公网安备 44130202000953号