如图所示,过圆
外一点
作它的一条切线,切点为
,过
点作直线
垂直于直线
,垂足为
.
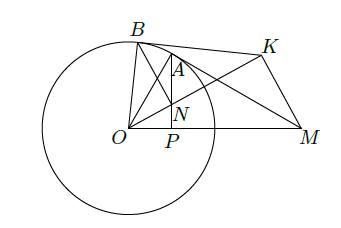
(1)证明:
;
(2)
为线段
上一点,直线
垂直于直线
,且交圆
于
点.过点
的切线交直线
于
.证明:
.
推荐套卷
如图所示,过圆
外一点
作它的一条切线,切点为
,过
点作直线
垂直于直线
,垂足为
.

(1)证明:
;
(2)
为线段
上一点,直线
垂直于直线
,且交圆
于
点.过点
的切线交直线
于
.证明:
.