对某电子元件进行寿命追踪调查,情况如下.
| 寿命(h) |
100—200 |
200—300 |
300—400 |
400—500 |
500—600 |
| 个数 |
20 |
30 |
80 |
40 |
30 |
(1)列出频率分布表;
(2)画出频率分布直方图;
(3)估计电子元件寿命在100—400 h以内的在总体中占的比例;
(4)估计电子元件寿命在400 h以上的在总体中占的比例.
相关知识点
推荐套卷
 中,已知
中,已知 ,
, ,求
,求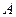 和
和 .
.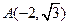 ,
,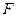 是椭圆
是椭圆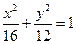 的右焦点,在椭圆上求一点
的右焦点,在椭圆上求一点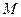 ,
,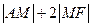 取得最小值.
取得最小值.
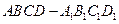 中,
中,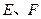 分别是
分别是 的中点.
的中点. 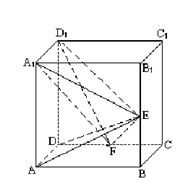
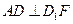 ;(2)求
;(2)求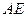 与
与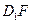 所成的角;
所成的角;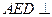 面
面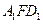 ;(4)
;(4) 的体积
的体积
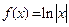
 ,函数
,函数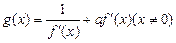
 时,求函数
时,求函数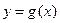 的表达式;
的表达式; ,函数
,函数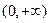 上的最小值是2 ,求
上的最小值是2 ,求 的值;
的值;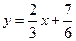 与函数
与函数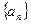 满足
满足 先计算前四项,猜想
先计算前四项,猜想 的表达式,并用数学归纳法证明.
的表达式,并用数学归纳法证明. 粤公网安备 44130202000953号
粤公网安备 44130202000953号