试判断下面的证明过程是否正确：
用数学归纳法证明：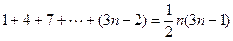
证明：（1）当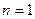
时，左边＝1，右边＝1
∴当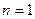时命题成立．
（2）假设当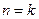
时命题成立，即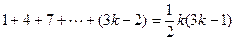
则当
时，需证
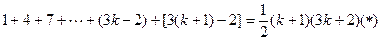
由于左端等式是一个以1为首项，公差为3，项数为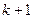
的等差数列的前
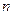项和，其和为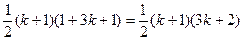
∴
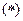式成立，即时，命题成立．根据（1）（2）可知，对一切
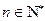，命题成立．
的值域.
的定义域.
的值.
求
的值.相关知识点
推荐套卷
试判断下面的证明过程是否正确：
用数学归纳法证明：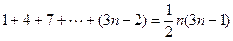
证明：（1）当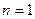时，左边＝1，右边＝1
∴当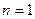时命题成立．
（2）假设当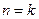时命题成立，即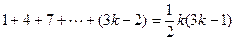
则当时，需证
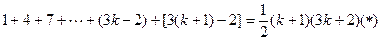
由于左端等式是一个以1为首项，公差为3，项数为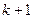的等差数列的前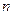项和，其和为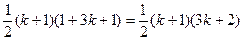
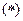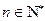∴式成立，即时，命题成立．根据（1）（2）可知，对一切，命题成立．
粤公网安备 44130202000953号