已知椭圆C的中心在原点,焦点在x轴上,它的一个顶点恰好是抛物线y=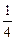 x2的焦点,离心率等于
x2的焦点,离心率等于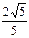 .
.
求椭圆C的方程;
过椭圆C的右焦点F作直线l交椭圆C于A、B两点,交y轴于M点,若
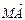 =λ1
=λ1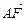 ,
,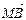 =λ2
=λ2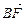 ,求证λ1+λ2为定值.
,求证λ1+λ2为定值.
推荐套卷
已知椭圆C的中心在原点,焦点在x轴上,它的一个顶点恰好是抛物线y=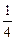 x2的焦点,离心率等于
x2的焦点,离心率等于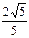 .
.
求椭圆C的方程;
过椭圆C的右焦点F作直线l交椭圆C于A、B两点,交y轴于M点,若
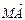 =λ1
=λ1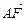 ,
,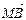 =λ2
=λ2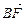 ,求证λ1+λ2为定值.
,求证λ1+λ2为定值.