(本小题满分12分)某食品企业一个月内被消费者投诉的次数用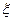
表示，
椐统计，随机变量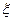的概率分布如下：
|
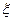0 |
1 |
2 |
3 |
| p |
0.1 |
0.3 |
2a |
a |
(Ⅰ)求a的值和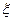的数学期望；
（Ⅱ）假设一月份与二月份被消费者投诉的次数互不影响,求该企业在这两个月内共被消费者投诉2次的概率。
的特征值．
的特征多项式．
，若矩阵M的逆矩阵M－1＝
，求a、b的值．
，N＝
，求MN.
(其中a>0，b>0)．
＋y2＝1，求a、b的值．推荐套卷
(本小题满分12分)某食品企业一个月内被消费者投诉的次数用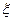表示，
椐统计，随机变量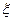的概率分布如下：
|
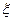0 |
1 |
2 |
3 |
| p |
0.1 |
0.3 |
2a |
a |
(Ⅰ)求a的值和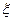的数学期望；
（Ⅱ）假设一月份与二月份被消费者投诉的次数互不影响,求该企业在这两个月内共被消费者投诉2次的概率。
粤公网安备 44130202000953号