如图，在锐角△ABC中，AB<AC，AD是边BC上的高，P是线段AD内一点。过P作PE⊥AC，垂足为E，做PF⊥AB，垂足为F。O1、O2分别是△BDF、△CDE的外心。求证：O1、O2、E、F四点共圆的充要条件为P是△ABC的垂心。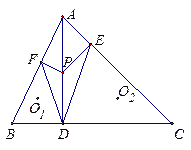
相关试题
，其中
，
，求角
的值；
，求
的值。
的最小正周期；
上的最大值，并求出
满足
，且在[-3，-2]上是减函数，若
是锐角三角形的两个内角，则
与
的大小关系为 ；
、
，
，求
的值；
，求
的值。
，
，求
；
的最大值。推荐套卷
如图，在锐角△ABC中，AB<AC，AD是边BC上的高，P是线段AD内一点。过P作PE⊥AC，垂足为E，做PF⊥AB，垂足为F。O1、O2分别是△BDF、△CDE的外心。求证：O1、O2、E、F四点共圆的充要条件为P是△ABC的垂心。
粤公网安备 44130202000953号