如图，已知平行六面体ABCD—A1B1C1D1的底面是菱形且∠C1CB=∠C1CD=∠BCD=60°,
(1)证明
C1C⊥BD；
(2)假定CD=2，CC1=
，记面C1BD为α,面CBD为β,求二面角α—BD—β的平面角的余弦值；
(3)当
的值为多少时，可使A1C⊥面C1BD？
经过
，且与点
和
的距离之比为
，求直线
，
，在
轴上找一点
，使
，并求
的值；
与
间的距离为
，求
与直线
，
分别交于点
，
，若
的中点是
，求直线
，且点
到该直线距离等于
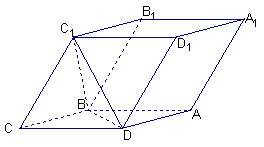
，求该直线倾斜角．推荐套卷
如图，已知平行六面体ABCD—A1B1C1D1的底面是菱形且∠C1CB=∠C1CD=∠BCD=60°,
(1)证明 C1C⊥BD；
(2)假定CD=2，CC1=，记面C1BD为α,面CBD为β,求二面角α—BD—β的平面角的余弦值；
(3)当的值为多少时，可使A1C⊥面C1BD？
粤公网安备 44130202000953号