设函数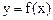
是定义在
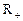上的函数，并且满足下面三个条件：（1）对正数x、y都有
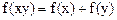；（2）当
时，
；（3）
。则
（Ⅰ）求
和
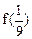的值；
（Ⅱ）如果不等式
成立，求x的取值范围．
（Ⅲ）如果存在正数k，使不等式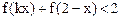
有解，求正数
的取值范围．
相关试题
=loga
(a＞0且a≠1)是奇函数
，（
，
图像；
的值；
时，求
，
为函数
的定义域，若
，求实数
的取值范围。
的厂房（不管墙高），工程的造价是：相关知识点
推荐套卷
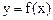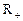设函数是定义在上的函数，并且满足下面三个条件：（1）对正数x、y都有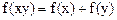；（2）当时，；（3）。则
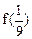（Ⅰ）求和的值；
（Ⅱ）如果不等式成立，求x的取值范围．
（Ⅲ）如果存在正数k，使不等式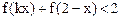有解，求正数的取值范围．
粤公网安备 44130202000953号