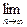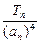设An为数列{an}的前n项和,An= (an-1),数列{bn}的通项公式为bn=4n+3;
(an-1),数列{bn}的通项公式为bn=4n+3;
(1)求数列{an}的通项公式;
(2)把数列{an}与{bn}的公共项按从小到大的顺序排成一个新的数列,证明:数列{dn}的通项公式为dn=32n+1;
(3)设数列{dn}的第n项是数列{bn}中的第r项,Br为数列{bn}的前r项的和;Dn为数列{dn}的前n项和,Tn=Br-Dn,求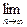

推荐套卷
设An为数列{an}的前n项和,An= (an-1),数列{bn}的通项公式为bn=4n+3;
(an-1),数列{bn}的通项公式为bn=4n+3;
(1)求数列{an}的通项公式;
(2)把数列{an}与{bn}的公共项按从小到大的顺序排成一个新的数列,证明:数列{dn}的通项公式为dn=32n+1;
(3)设数列{dn}的第n项是数列{bn}中的第r项,Br为数列{bn}的前r项的和;Dn为数列{dn}的前n项和,Tn=Br-Dn,求