已知函数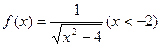
.(Ⅰ) 求f –1(x)；(Ⅱ) 若数列{an}的首项为a1=1，
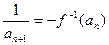(nÎN+)，求{an}的通项公式an；(Ⅲ) 设bn=an+12+an+22+¼+a2n+12，是否存在最小的正整数k，使对于任意nÎN+有bn<
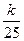成立.若存在，求出k的值；若不存在，说明理由.
推荐套卷
已知函数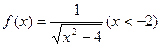.(Ⅰ) 求f –1(x)；(Ⅱ) 若数列{an}的首项为a1=1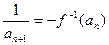，(nÎN+)，求{an}的通项公式an；(Ⅲ) 设bn=an+12+an+22+¼+a2n+12，是否存在最小的正整数k，使对于任意nÎN+有bn<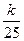成立.若存在，求出k的值；若不存在，说明理由.
粤公网安备 44130202000953号