如图，点A、B、C都在函数y=
的图像上，它们的横坐标分别是a、a+1、a+2
又A、B、C在x轴上的射影分别是A′、B′、C′,记△AB′C的面积为f(a),△A′BC′的面积为g(a).
(1)求函数f(a)和g(a)的表达式；
(2)比较f(a)与g(a)的大小，并证明你的结论.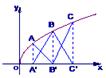
，求不等式
的解集
Rl，其中R为扇形半径，l为弧长）
；
，试确定实数的取值范围
,求y关于t的函数关系式,t的范围.推荐套卷
如图，点A、B、C都在函数y=的图像上，它们的横坐标分别是a、a+1、a+2 又A、B、C在x轴上的射影分别是A′、B′、C′,记△AB′C的面积为f(a),△A′BC′的面积为g(a).
(1)求函数f(a)和g(a)的表达式；
(2)比较f(a)与g(a)的大小，并证明你的结论.
粤公网安备 44130202000953号