已知函数f(x)的定义域为R，且对m、n∈R,恒有f(m+n)=f(m)+f(n)－1,且f(－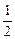
)=0,当x>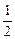－时，f(x)>0.
(1)求证:f(x)是单调递增函数；
(2)试举出具有这种性质的一个函数，并加以验证.
相关知识点
推荐套卷
已知函数f(x)的定义域为R，且对m、n∈R,恒有f(m+n)=f(m)+f(n)－1,且f(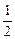－)=0,当x>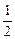－时，f(x)>0.
(1)求证:f(x)是单调递增函数；
(2)试举出具有这种性质的一个函数，并加以验证.
粤公网安备 44130202000953号