设函数f (x) =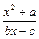
(b，c∈N*)，若方程f(x) = x的解为0，2，且f (–2)＜–
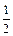．（Ⅰ）试求函数f(x)的单调区间；（Ⅱ）已知各项不为零的数列{an}满足4Sn·f (
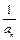) = 1，其中Sn为{an}的前n项和．求证：
．
)的值；
∈(0，
)，f (
)＝
，求cos2
<
<
<
,
的值.（Ⅱ）求
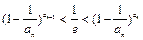），且a⊥b． 求tanα的值；推荐套卷
设函数f (x) =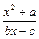(b，c∈N*)，若方程f(x) = x的解为0，2，且f (–2)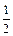＜–．（Ⅰ）试求函数f(x)的单调区间；（Ⅱ）已知各项不为零的数列{an}满足4Sn·f (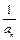) = 1，其中Sn为{an}的前n项和．求证：．
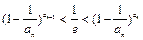粤公网安备 44130202000953号