（本小题满分12分）
已知，椭圆C以过点A（1，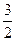
），两个焦点为（－1，0）（1，0）。
（1） 求椭圆C的方程；
（2） E,F是椭圆C上的两个动点，如果直线AE的斜率与AF的斜率互为相反数，证明直线EF的斜率为定值，并求出这个定值。 
相关试题
与
，
，
所围成的平面图形的面积。
，直线
，
为平面上的动点，过
的垂线，垂足为点
，且
.
的方程；
的直线交轨迹
，
两点，交直线
，已知
，求
的值.
与函数
.
的图象在点
处有公共的切线，求实数
的值；
，求函数
的极值.
垂足为
，
是
的中点且
，
，
.
平面
；
与平面
的首项
，
，
…．
是等比数列；（Ⅱ）求数列
的前
项和
推荐套卷
（本小题满分12分）
已知，椭圆C以过点A（1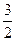，），两个焦点为（－1，0）（1，0）。
（1） 求椭圆C的方程；
（2） E,F是椭圆C上的两个动点，如果直线AE的斜率与AF的斜率互为相反数，证明直线EF的斜率为定值，并求出这个定值。
粤公网安备 44130202000953号