(本小题满分12分)
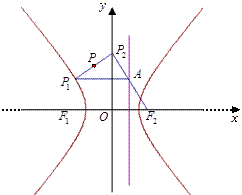
已知点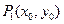 为双曲线
为双曲线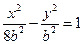 (
(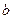 为正常数)上任一点,
为正常数)上任一点,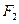 为双曲线的右焦点,过
为双曲线的右焦点,过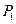 作右准线的垂线,垂足为
作右准线的垂线,垂足为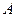 ,连接
,连接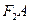 并延长交
并延长交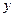 轴于
轴于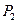 .
. 

(1) 求线段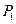
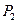 的中点
的中点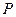 的轨迹
的轨迹 的方程;
的方程;
(2) 设轨迹 与
与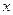 轴交于
轴交于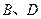 两点,在
两点,在 上任取一点
上任取一点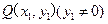 ,直线
,直线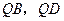 分别交
分别交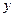 轴于
轴于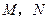 两点.求证:以
两点.求证:以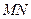 为直径的圆过两定点.
为直径的圆过两定点.
推荐套卷
(本小题满分12分)

已知点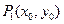 为双曲线
为双曲线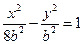 (
(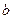 为正常数)上任一点,
为正常数)上任一点,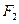 为双曲线的右焦点,过
为双曲线的右焦点,过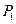 作右准线的垂线,垂足为
作右准线的垂线,垂足为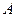 ,连接
,连接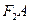 并延长交
并延长交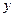 轴于
轴于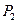 .
. 

(1) 求线段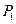
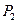 的中点
的中点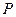 的轨迹
的轨迹 的方程;
的方程;
(2) 设轨迹 与
与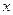 轴交于
轴交于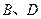 两点,在
两点,在 上任取一点
上任取一点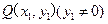 ,直线
,直线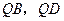 分别交
分别交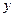 轴于
轴于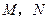 两点.求证:以
两点.求证:以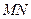 为直径的圆过两定点.
为直径的圆过两定点.